Abstract:
This paper examines the oscillations of a spherical pendulum with horizontal Lissajous excitation. The pendulum has two degrees of freedom: a rotational angle defined in the horizontal plane and an inclination angle defined by the pendulum with respect to the vertical z axis. The results of numerical simulations are illustrated with the mathematical model in the form of multi-colored maps of the largest Lyapunov exponent. The graphical images of geometrical structures of the attractors placed on Poincare´ cross sections are shown against the maps of the
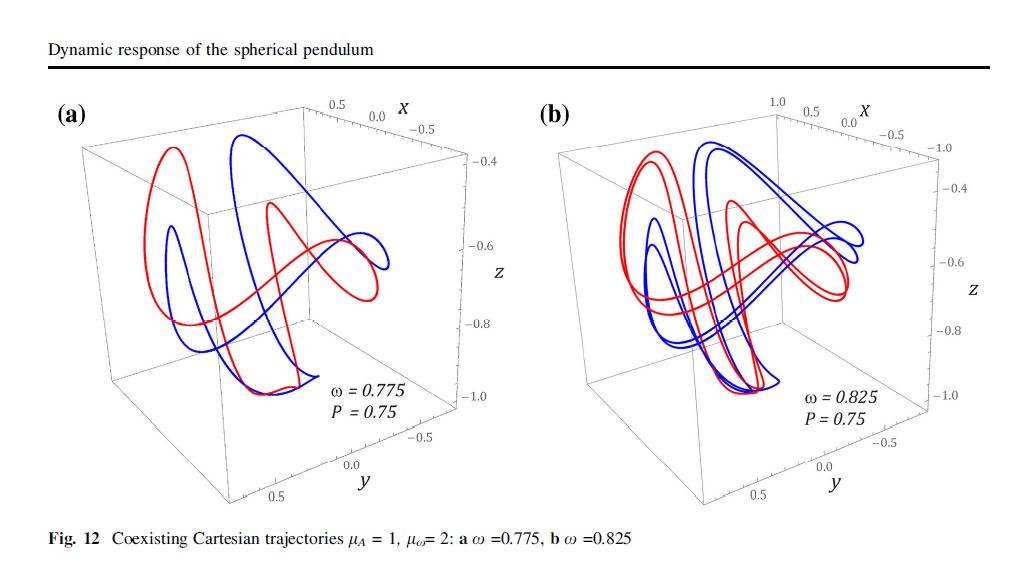
resolution density of the trajectory points passing through a control plane. Drawn for a steady-state, the graphical images of the trajectory of a tip mass are shown in a three-dimensional space. The obtained trajectories of the moving tip mass are referred to a constructed bifurcation diagram.
Authors: Grzegorz Litak . Jerzy Margielewicz . Damian Ga˛ska . Daniil Yurchenko .
Krzysztof Da˛bek
This paper was published in Nonlinear Dynamics, Issue 3, November 2020, Vol.102
To read full text, please visit publisher site or download pdf file.
| This work was supported by the program of the Ministry of Science and Higher Education in Poland under the project DIALOG 0019/DLG/2019/10 in the years 2019-2021. |